Overview:
In this post, a direct stiffness method based solver is discussed for 2D linear truss systems.
Consider the following truss structure.
The Global Member Stiffness Matrix as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Global Member Stiffness Matrix
def K_ele(n):
Length = L[n]
Angle = theta[n]
c = math.cos(Angle)
s = math.sin(Angle)
K11 = (E*A/Length)*np.array([[c**2,c*s],[c*s,s**2]])
K12 = (E*A/Length)*np.array([[-c**2,-c*s],[-c*s,-s**2]])
K21 = (E*A/Length)*np.array([[-c**2,-c*s],[-c*s,-s**2]])
K22 = (E*A/Length)*np.array([[c**2,c*s],[c*s,s**2]])
return [K11, K12, K21,K22]
Formulation of the stiffness matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#Primary Stiffness Matrix
Kp = np.zeros([nDoF,nDoF])
n = 0
for mbr in members:
[K11,K12,K21,K22] = K_ele(n)
n = n + 1
node_i=mbr[0].astype(int)
node_j=mbr[1].astype(int)
Kp[2*node_i-2:2*node_i-1+1,2*node_i-2:2*node_i-1+1] = Kp[2*node_i-2:2*node_i-1+1,2*node_i-2:2*node_i-1+1] + K11
Kp[2*node_i-2:2*node_i-1+1,2*node_j-2:2*node_j-1+1] = Kp[2*node_i-2:2*node_i-1+1,2*node_j-2:2*node_j-1+1] + K12
Kp[2*node_j-2:2*node_j-1+1,2*node_i-2:2*node_i-1+1] = Kp[2*node_j-2:2*node_j-1+1,2*node_i-2:2*node_i-1+1] + K21
Kp[2*node_j-2:2*node_j-1+1,2*node_j-2:2*node_j-1+1] = Kp[2*node_j-2:2*node_j-1+1,2*node_j-2:2*node_j-1+1] + K22
#Apply Boundary Conditions
deleteRowcolumn = []
for delete in restrainedDoF:
deleteRowcolumn.append(delete-1)
Ks = np.delete(Kp,(deleteRowcolumn), axis=0)
Ks = np.delete(Ks,(deleteRowcolumn), axis=1)
Summarizing the output results:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
REACTIONS
Reaction at DoF 1: 6.08 kN
Reaction at DoF 2: 62.5 kN
Reaction at DoF 37: -6.08 kN
Reaction at DoF 38: 62.5 kN
MEMBER FORCES
Member 1 Force: -80.74 kN
Member 2 Force: 19.23 kN
Member 3 Force: -28.55 kN
Member 4 Force: -63.83 kN
Member 5 Force: 14.87 kN
Member 6 Force: -6.64 kN
Member 7 Force: -25.92 kN
Member 8 Force: -49.85 kN
Member 9 Force: 39.61 kN
Member 10 Force: -33.58 kN
Member 11 Force: -0.52 kN
Member 12 Force: 26.89 kN
Member 13 Force: -41.48 kN
Member 14 Force: -17.57 kN
Member 15 Force: 13.74 kN
Member 16 Force: -6.67 kN
Member 17 Force: 38.04 kN
Member 18 Force: -41.25 kN
Member 19 Force: -6.67 kN
Member 20 Force: -41.25 kN
Member 21 Force: 13.74 kN
Member 22 Force: 26.89 kN
Member 23 Force: -41.48 kN
Member 24 Force: -17.57 kN
Member 25 Force: -0.52 kN
Member 26 Force: -49.85 kN
Member 27 Force: 39.61 kN
Member 28 Force: -33.58 kN
Member 29 Force: -25.92 kN
Member 30 Force: -63.83 kN
Member 31 Force: 14.87 kN
Member 32 Force: -6.64 kN
Member 33 Force: -28.55 kN
Member 34 Force: -80.74 kN
Member 35 Force: 19.23 kN
NODAL DISPLACEMENTS
Node 1: Ux = 0.0 m, Uy = 0.0 m
Node 2: Ux = -0.00143 m, Uy = -0.00032 m
Node 3: Ux = -0.0013 m, Uy = -0.0003 m
Node 4: Ux = -0.00114 m, Uy = -0.00063 m
Node 5: Ux = -0.00082 m, Uy = -0.00032 m
Node 6: Ux = -0.00041 m, Uy = -0.00133 m
Node 7: Ux = 8e-05 m, Uy = -0.00109 m
Node 8: Ux = -0.00011 m, Uy = -0.00212 m
Node 9: Ux = 0.00018 m, Uy = -0.00181 m
Node 10: Ux = 0.0 m, Uy = -0.00224 m
Node 11: Ux = 0.00011 m, Uy = -0.00212 m
Node 12: Ux = -0.00018 m, Uy = -0.00181 m
Node 13: Ux = 0.00041 m, Uy = -0.00133 m
Node 14: Ux = -8e-05 m, Uy = -0.00109 m
Node 15: Ux = 0.00114 m, Uy = -0.00063 m
Node 16: Ux = 0.00082 m, Uy = -0.00032 m
Node 17: Ux = 0.00143 m, Uy = -0.00032 m
Node 18: Ux = 0.0013 m, Uy = -0.0003 m
Node 19: Ux = 0.0 m, Uy = 0.0 m
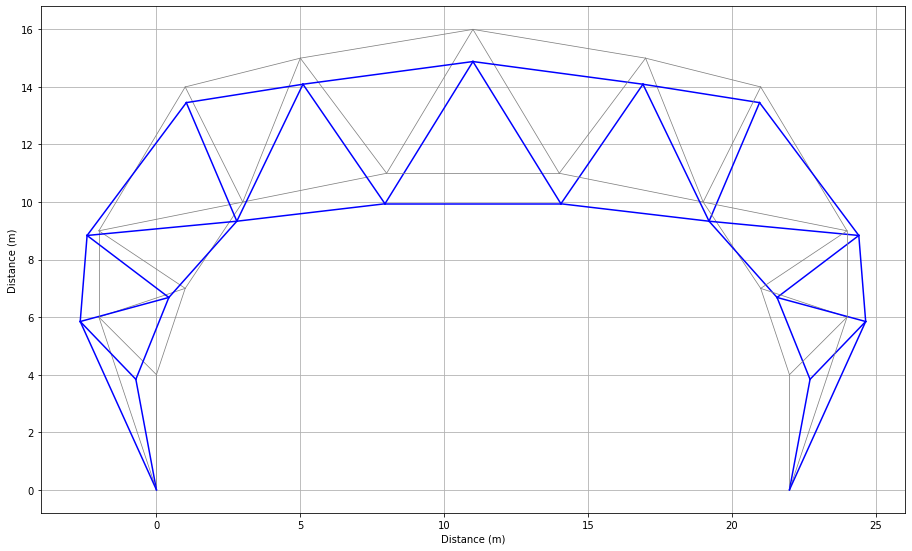Deformed Plot (Magnification Factor = 500)ETABS Verification
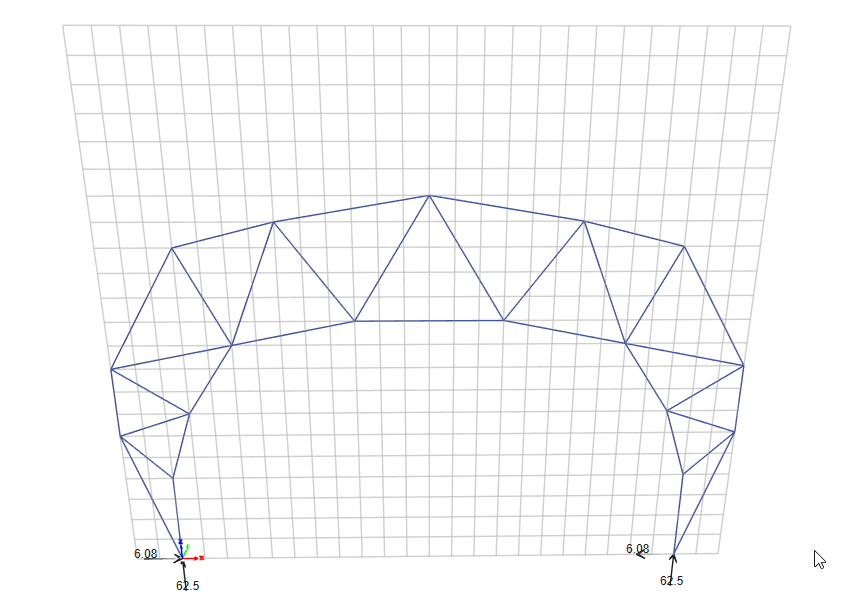Restraint reactions
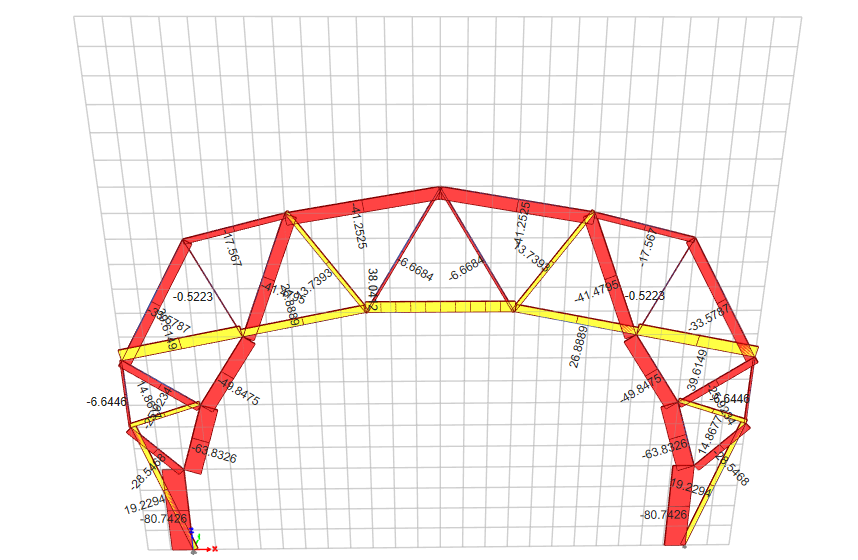Axial force diagram